Blog

Mình chợt nhận ra là trong các parabol của hàm bậc 2 với dạng tổng quát f(x) = Ax^2+Bx+C (A\neq0), nếu A\ge0 thì parabol có dạng “U thường” – đáy ở phía dưới, tức có cực tiểu. Còn nếu A<0 thì parabol có dạng “U lộn ngược” – đỉnh ở phía trên, tức có cực đại.

Xét thấy đây là một tính chất khá thú vị nên trong bài này, mình sẽ trình bày chi tiết cách chứng minh tính chất này.

Xét hàm bậc 2:

f(x) = Ax^2+Bx+C (A\neq0)

Ta có phương trình tương đương:

f(x)=A\left(x^2+\frac{B}{A}x\right)+C\, \, (1)

Xét biểu thức trong ngoặc:

x^2+\frac{B}{A}x \\
\begin{aligned}
&= x^2 + 2x\frac{B}{2A}+\frac{B^2}{4A^2}-\frac{B^2}{4A^2} \\
&= \left(x+\frac{B}{2A}x\right)^2-\left(\frac{B}{2A}\right)^2
\end{aligned}

Thay vào (1) ta có:

\begin{aligned}
f(x)&=A\left(x^2+\frac{B}{A}x\right)+C\\
\Leftrightarrow f(x)&=A\left[ \left(x+\frac{B}{2A}x\right)^2-\left(\frac{B}{2A}\right)^2 \right] + C \\
\Leftrightarrow f(x)&=A\left(x+\frac{B}{2A}x\right)^2 - \frac{B^2}{4A} + C \\
\Leftrightarrow f(x)&=A\left(x+\frac{B}{2A}x\right)^2 - \frac{B^2-4AC}{4A} \\
\end{aligned}

Vì \frac{B^2-4AC}{4A} là một hằng số không đổi (trên thực tế, các phương trình đã cho biết trước giá trị của A, B, C) nên độ lớn/ nhỏ của hàm f(x) phụ thuộc vào vế A\left(x+\frac{B}{2A}x\right)^2.

Nếu A>0 thì A\left(x+\frac{B}{2A}x\right)^2 sẽ có cực tiểu tại 0. Cụ thể:

A\left(x+\frac{B}{2A}\right)^2\geq0
\rightarrow Min\left(x+\frac{B}{2A}\right)=0\, tại\, x=\frac{-B}{2A}

Ngược lại, nếu A<0 thì A\left(x^2+\frac{B}{2A}x\right)^2 sẽ có cực đại tại 0. Cụ thể:

A\left(x+\frac{B}{2A}\right)^2\leq0
\rightarrow Max\left(x+\frac{B}{2A}\right)=0\, tại\, x=\frac{-B}{2A}

Và điểm đặc biệt là dù cực đại hay cực tiểu, thì y=-\frac{B^2-4AC}{4A} tại x=\frac{-B}{2A}.

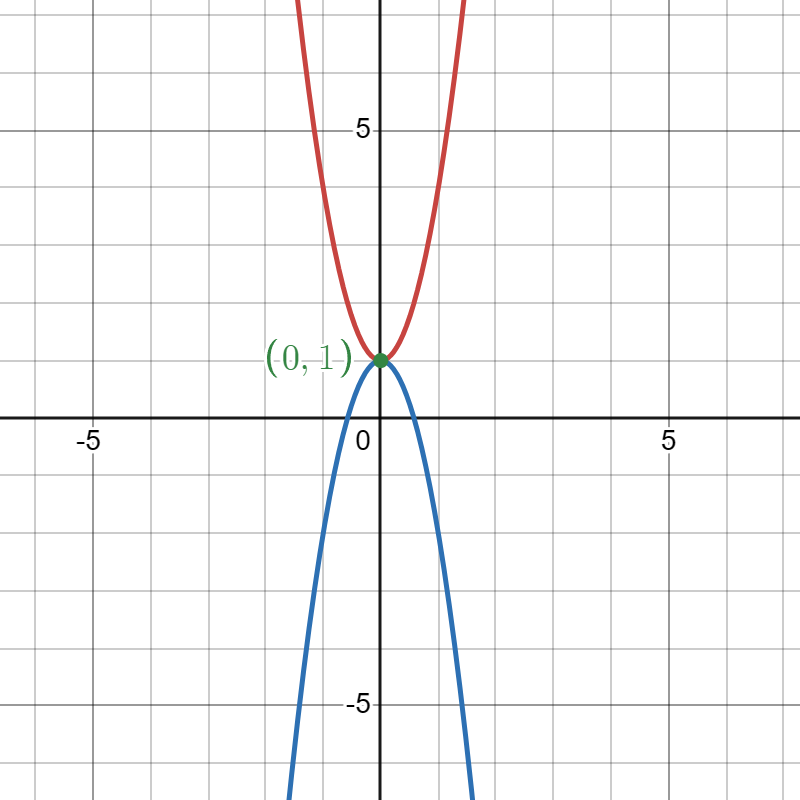
Đồ thị hàm số y=3x^2+1 (đỏ) và y’=3x^2+1 (xanh) với điểm cực đại/ cực tiểu chung 1 tọa độ (0,1).